Framåtriktade neurala nätverk, på engelska feed-forward neural networks, är den enklaste typen av neuralt nätverk. Det kallas framåtriktat eftersom beräkningen sker iterativt från ett neuronlager till ett annat utan att något skickas tillbaka (Jurafsky & Martin 2019: kap 7: sida 1). Som tidigare nämnts är neurala nätverk i grund och botten uppbyggda av logistiska regressionsklassificerare. Men det finns två särskiljande egenskaper.

Logistisk regression innebär att ta den inre produkten (eng. dot product) av en indatavektor och en viktmatris samt applicera en normaliserad sigmoid-funktion (t.ex. softmax) för att generera en sannolikhetsdistribution som summerar till 1. Ett neuralt nätverk lägger till ett eller flera gömda lager mellan inputvektorerna och softmax-utdatat. Detta gör det möjligt för nätverket att i princip lära sig vilken funktion som helst.

Med logistiska regressionsklassificerare bestämmer man själv vilka features som ska användas genom kunskap om domänet. Men när man arbetar med neurala nätverk är det istället vanligare att låta nätverket själv avgöra vilka features som är relevanta för klassificieringen, så kallad representationsinlärning. Djupa nätverk (eng. deep nets), dvs. nätverk med flera lager, lämpar sig särskilt väl för just representationsinlärning.

Den här arkitekturen innebär att utdatat i varje lager går igenom en aktiveringsfunktion som omvandlar den till indata för ett annat lager. Genom icke-linjära aktiveringsfunktioner kan man fånga upp komplexa mönster i datat som inte låter sig uttryckas linjärt (Jain 2019). Det förhindrar också att utdatavärdet blir för högt genom att hålla det inom en viss kravspecificerad gräns (ibid).

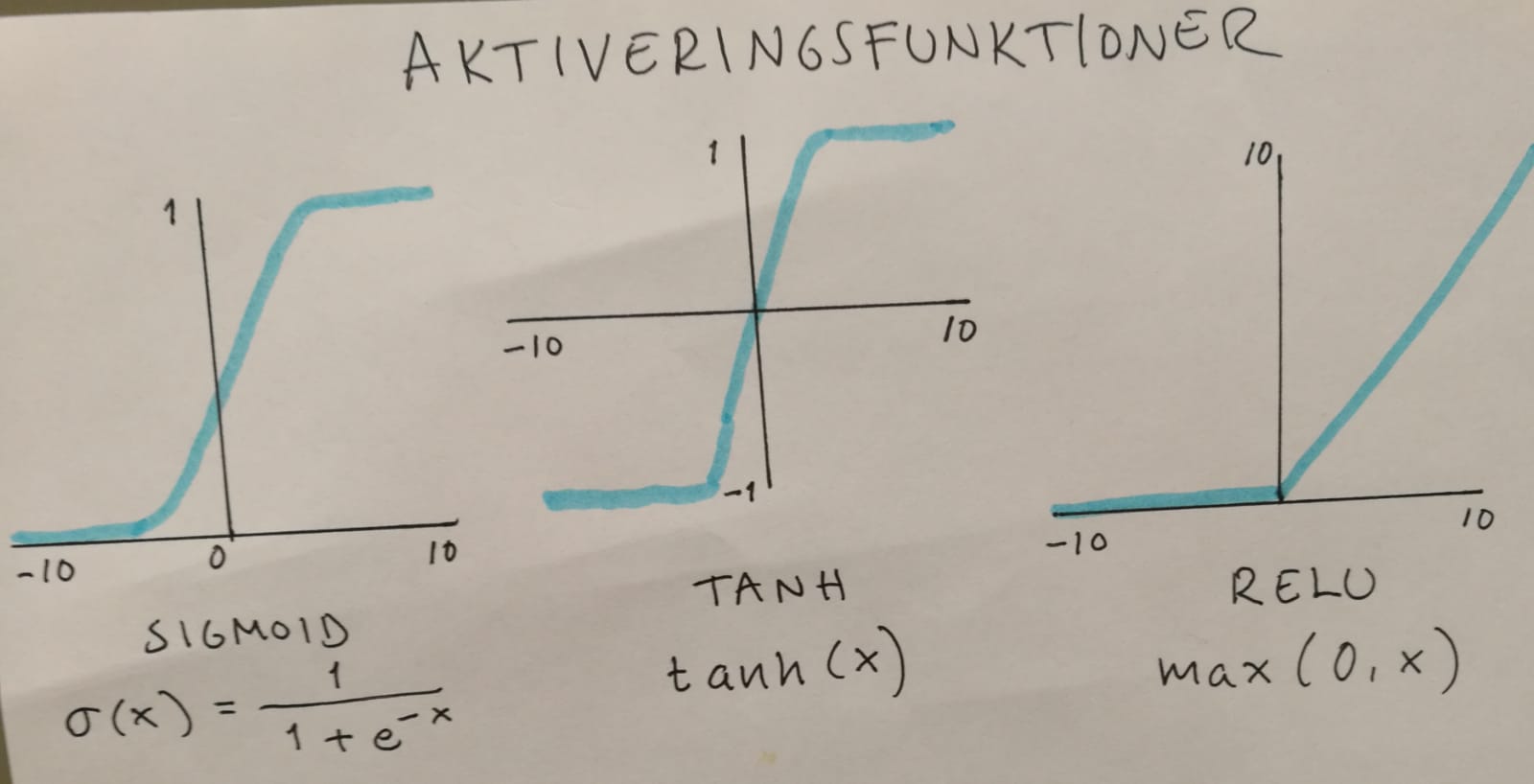
Tre populära icke-linjära aktiveringsfunktioner är sigmoid, tanh och den stegvis linjära aktiveringsfunktionen ReLU. Sigmoid används i praktiken inte som aktiveringsfunktion utan lämpar sig bättre för binära klassificeringsuppgifter (ibid). Tanh är en variant av sigmoid – “very similar but always better” (Jurafsky & Martin 2019: kap 7: sida 2) – som går från -1 till +1. Men den enklaste och kanske mest använda aktiveringsfunktionen är ReLU, som är densamma som inputsvektorn x när x är positiv, annars 0 (Jurafsky & Martin 2019: kap 7: sida 3). Rao & Brian skriver i “Natural Language Processing with PyTorch” (2019:43): “In fact, one could venture as far as say to say that many of the recent innovations in deep learning would’ve been impossible without the use of ReLU.”

När neurala nätverk uppdaterar sina vikter under upplärningen skickas felgradienten tillbaka genom nätet, från utdatalagret till indatalagret (s.k. backpropagation). Problemet är bara att med många lager så minskas gradienten markant när den skickas tillbaka, vilket kan kan göra det svårt att veta hur vikterna i neuronlagren närmast inmatningslagret ska justeras (Brownlee 2019). Detta kallas vanishing gradient descent-problemet och ReLU är just en av de lösningar som finns för att råda bot på det.

Med sigmoid och tanh riskerar man att få värden av w·x+b som är mättade (eng. saturated), dvs. väldigt nära 1, men “[r]ectifiers don’t have this problem, since the output of values close to 1 also approaches 1 in a nice gentle linear way” (Jurafsky & Martin 2019: kap 7: sida 4). Nackdelen är bara det s.k. “dying ReLU”-problemet i och med att alla negativa indatavärden sätts till 0: “[…] over time certain inputs in the network can simply become zero and never revive again” (Rao & Brian 2019:44).

Men tillbaka till de framåtriktade neurala nätverken som helhet. De består alltså av tre olika noder: inmatningsenheter, gömda enheter och utmatningsenheter. I standardutformningen är varje lager helt ihopkopplat – fully-connected – med intilliggande lager, vilket innebär att varje enhet (neuron) i varje lager tar som indata utdatat från alla enheter i föregående lager: “[t]hus each hidden unit sums over all the input units” (Jurafsky & Martin 2019: kap 7: sida 7). Varje enhet i det gömda lagret har en viktparameter w och bias-paremeter b. Tillsammans bildar dessa parameterar en viktmatris W och en ensam bias-vektor b för hela lagret. Detta möjliggör effektiva beräkningar via matrisoperationer.

Antalet utmatningsnoder (neuroner) beror på uppgiften. Vid binär klassificering har man ofta bara en utmatningsnod vars värde y är en sannolikhet av endera värden. Vid flerklassklassificering har man ofta flera utmatningsnoder – en för varje klass – vars samlade utdata tillsammans bildar en sannolikhetsdistribution över de olika klasserna. Precis som det gömda lagret har utmatningslagret en egen viktmatris W vars inre produkt med indatavektorn h ger ett utdata z som måste normaliseras för att bilda en tillåten sannolikhetsdistribution som kan summeras till 1. Detta kan vi göra med softmax-funktionen: softmax(z).

När man pratar om lagren i neurala nätverk brukar man inte räkna med indata-lagret. Ett neuralt nätverk med ett enda gömt lager bildar alltså tillsammans med utdata-lagret ett två-lagrigt nätverk.