Kontextfri grammatik (eng. CFG, context-free grammar) är en slags formell grammatik som grundar sig i konstituenter, dvs. idén om att grupper av ord beter sig som fristående enheter som kan bytas ut eller flyttas runt. Den består av regler som sätter ramarna för hur symboler i språket kan sättas samman, samt ett lexikon av ord och symboler. Symbolerna inom CFG delas in i två klasser: terminala och icke-terminala symboler. Terminala symboler är symboler som motsvarar ord i språket (genom lexikonet), medan icke-terminala symboler är symboler som uttrycker kluster eller generaliseringar.

Varje kontextfri grammatik består av ett högerled med en enda icke-terminal symbol, medan vänsterledet efter pilen (–>) är en ordnad lista bestående av en eller flera terminaler och icke-terminaler. Utöver regler (R), en uppsättning icke-terminala symboler (N), en uppsättning terminala symboler (Σ) finns en fjärde parameter som styr kontextfria grammatiker: startsymbolen S, som ofta avser en satsnod. Meningar som kan härledas ur en grammatik definieras av den grammatiken, och är därmed grammatiska, annars ogrammatiska. Terman generativ grammatik avser användandet av formella språk för att definiera en uppsättning möjliga meningar/strängar genererade av grammatiken.

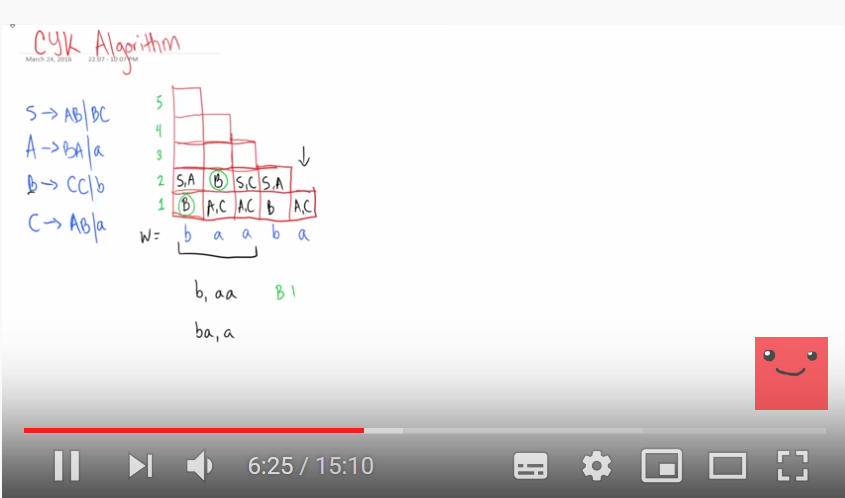
Två grammatiker är ekvivalenta om de genererar samma uppsättning strängar. Man pratar om stark ekvivalens (eng. strong equivalence) om de genererar samma strängar och tillskriver varje mening samma frasstruktur, och svag ekvivalens (eng. weak equivalence) om de enbart genererar samma strängar. Alla kontextfria grammatiker kan göras om till en Chomsky-normalform, vilket innebär att högerledet i varje regel enbart har två icke-terminala symboler eller en ensam terminal. Fördelen med detta är att det möjliggör skapandet av binära träd och därigenom användandet av enklare och effektivare parsningsalgoritmer, t.ex. CYK-algoritmen. CYK (förkortning för Cocke-Younger-Kasami) kan användas för att avgöra om en given sträng är grammatisk eller inte (utifrån en given kontextfri grammatik) genom att dela upp strängen i understrängar vars giltighet kontrolleras. Klicka på bilden nedan för att komma till en pedagogisk Youtube-video om hur CYK-algoritmen fungerar.

För att mäta kraften eller snarare komplexiteten i de formella mekanismer (ändliga automater, transduktorer, kontext-fria grammatiker, Markov-modeller mm.) som står till vårt förfogande, använder man sig av något som kallas Chomsky-hierarki. Den beskriver den generativa kraften hos olika grammatiker genom att rangordna dem i fyra-fem olika sorters språk som de kan generera, där de mindre komplexa blir undertyper till de mer komplexa. Den minst komplexa undergruppen är i den här modellen de reguljära språken, som har produktionsregler av typen A –> xB och A –> x och kan genereras av ändliga automater. Den något mer komplexa språktypen är de kontextfria språken som kan genereras av kontextfria grammatiker och tillåter vilken icke-terminal symbol som helst att skrivas om till en sträng av terminaler och icke-terminaler (A –> γ, där γ är en arbiträr sträng av terminaler och icke-terminaler).

Nästa språkgrupp är de milt kontext-känsliga språken, som inte ingår i originalhierarkin men som kan användas för att beskriva formalismer som CCG (eng. combinatory categorial grammar) och TAG (eng. tree-adjoining grammar). De milt kontext-känsliga språken är mindre komplexa än de konext-känsliga språken, som karaktäriseras av regler som skriver om en icke-terminal symbol A i kontexten αAβ till vilken icke-tom symbolsträng som helst (αγβ). Ytterligare ett steg uppåt i hierarkin hittar vi de rekursivt uppräkningsbara språken (eng. recursively enumerable languages), som också kallas Turing-ekvivalenta eftersom deras strängar kan räknas upp av en Turing-maskin. Dessa språk har inga begräsningar i sina regler, utan vilken icke-tom sträng som helst kan skrivas om till vilken annan sträng som helst.

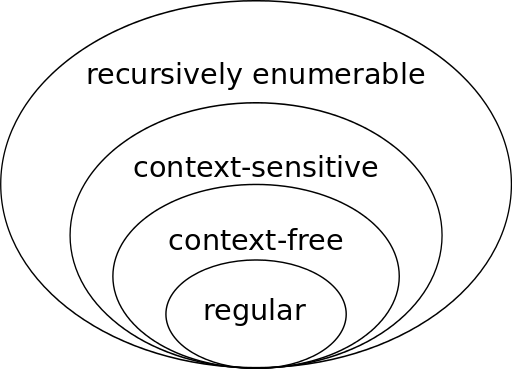
Chomsky-hierarkin visar fyra olika sorters språk av skiftande komplexitet. (Bild: J. Finkelstein [CC BY-SA 3.0], via Wikimedia Commons)

Det är av intresse att veta vilken av dessa typer som ett givet system faller under för att veta hur vi ska behandla det. Om det som vi vill kunna generera eller parsa är regelbundet, kan vi till exempel använda oss av reguljära uttryck och ändliga automater för att processa reglerna. Lyckligtvis finns det metoder för att avgöra detta. Det bästa sättet att bevisa om ett språk är regelbundet eller inte är genom att försöka skapa reguljära uttryck för det. Men om man vill visa att det språk inte är regelbundet kan man använda sig av ett pumplemma (eng. pumping lemma). Pumplemmat beskriver en egenskap hos reguljära språk som innebär att en tillräckligt lång sträng i språket kan pumpas upp - dvs. att någon del innuti strängen kan upprepa sig. Denna egenskap finns även hos icke-reguljära språk, men eftersom den är nödvändig för reguljära språk kan avsaknaden av den åtminstone användas för att avgöra om ett språk inte är reguljärt.