De finns flera olika metoder för dependensparsning, bl.a. dynamisk programmering (Eisner-algoritmen), regelstyrd parsning och transitionsbaserad parsning (som behandlats i tidigare inlägg). Grafbaserad parsning är en fjärde metod som involverar letandet efter ett dependensträd som uppfyller ett visst värde i ett grafsystem med viktade kanter (verkar också kunna kallas bågar) som innefattar alla möjliga variationer av träd.

En av fördelarna som nämns med de grafbaserade metoderna i Jurafsky & Martin (2019) är att de kan producera icke-projektiva träd, vilket är värdefullt för många språk som har en annan satsstruktur än engelskan (t.ex. tjeckiska och hindi). Dessutom erbjuder de högre parsningsriktighet i meningar med längre dependenser, eftersom de ser till hela träd, och inte tar giriga, lokala parsningsbeslut som de transitionsbaserade modellerna.

Jurafsky & Martin (2019) beskriver mer ingående den grafbaserade maximalt utspännande träd-algortimen (eng. maximal spanning tree) som används på riktade, viktade grafer. För en given mening konstruerar man en “fully-connected, weighted, directed graph where the vertices are the input words and the directed edges represent all possible head-dependent assignments” (ibid:18). Vikterna i grafen motsvarar poängen för varje huvud-dependent-relation enligt det träningsdata som ligger till grund.

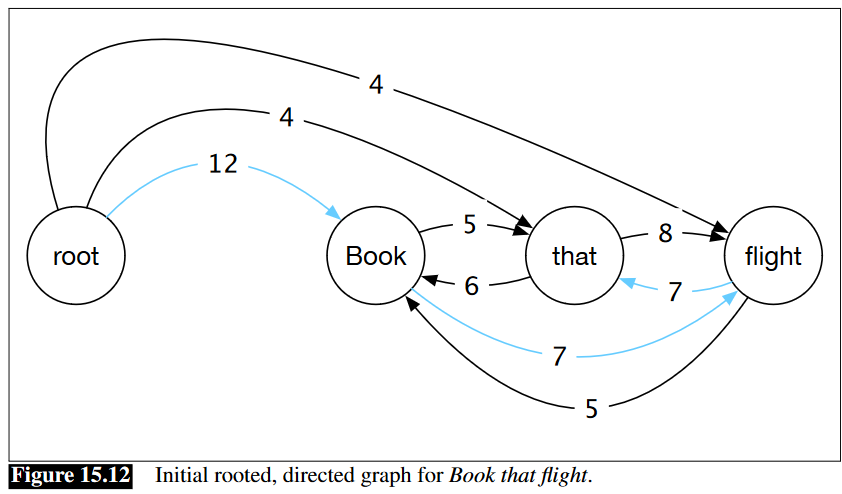
Maximum spanning tree applicerad på strängen "Book that flight" (Jurafsky & Martin 2019).

För varje nod (eng. vertex) i det utspännande trädet väljer algoritmen en och endast en inkommande kant/båge som representerar en möjlig huvud-deklarering utifrån den kant/båge som har störst vikt. Om de valda kanterna resulterar i ett utspännande träd har man lyckats hitta det mest troliga dependensträdet för inputsträngen. Problem kan uppstå om de valda kanterna innehåller cykler. Chu-Liu-Edmonds-algoritmen är en annan algoritm, utvecklad på 60-talet, som löser detta genom att den “[…] begins with a greedy selection and follows with an elegant recursive cleanup phase that eliminates cycles” (Jurafsky & Martin 2019:19).