Inom kursen Komputationell semantik (LT2213) konfronterades vi i förra veckan med något nytt och läskigt: lambdakalkyl (eng. lambda calculus). Sedan dess har jag skjutit upp att sätta mig in i det på allvar, men eftersom vi har en inlämningsuppgift på ämnet som strax måste in tänkte jag ta kvällen i akt och läsa på så mycket som möjligt innan jag går och lägger mig. Nu kör vi!

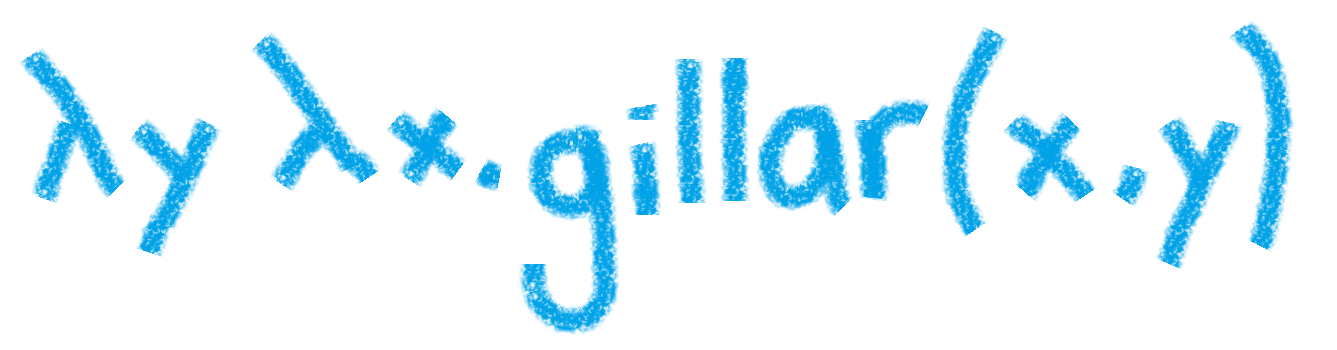
Vi börjar med lite historia. Lambdakalkyl definieras på svenska Wikipedia som ett “formellt system som skapades för att undersöka funktioner och rekursion”. Som upphovsman räkans den amerikanske matematikern och logikern Alonzo Church (1903-1995) som arbetade fram systemet på 1930-talet. Han har också gjort sig känd för Church-Turings hypotes, som säger att en matematisk funktion är effektivt beräkningsbar om och endast om den kan beräknas med hjälp av en algoritm på en Turing-maskin.[1] Men det var en annan amerikan, Richard Montague (1930-1971), som introducerade lambdakalkylen till lingvistiken.

Så vad ska lambdakalkyl överhuvudtaget vara bra för inom språkteknologin? Videon nedan ger en bra introduktion, men i kort så handlar det om att enklare kunna utvärdera sanningsvärden i meningar (vilket är ju kärnan av semantiken) genom att ta bryta upp stora semantiska uttryck/funktioner i mindre sådana - en teknik kallad currying.

När man har en mening i naturligt språk, t.ex. “Anna gillar äpplen” så kan den delas upp i ett syntaktiskt träd där nominalfrasen (NP) har en undernod, Anna, och verbfrasen (VP) “gillar äpplen” två stycken: gillar och äpplen. När vi sedan vill konstruera vår semantiska representation av meningen börjar vi från undernoderna i VP:t och märker på en gång att predikatet gillar kräver två variabler, en som gillar och något som gillas: gillar(x,y).

För att lösa detta beräkningsmässigt bryter vi ut x:et och y:et till ett lambdauttryck, så att vi kan hålla till godo innan vi når objektet äpplen och nominalfrasen Anna: λy λx.(gillar(x,y). Placeringen av lambda-y innan lambda-x innebär att y:et är den första variabeln som pluggas in i funktionen, som då får formen λx.gillar(x,äpplen), innan vi går vidare och pluggar in subjektvariabeln x. Genom att sätta x till Anna – som i λx.gillar(x,äpplen)(Anna) – kan vi reducera uttrycket ytterligare till: gillar(Anna,äpplen).

Med kvantifikatorer utökar vi komplexiteten i vår semantiska representation. Eftersom fria variabler som ackompagneras av universalkvantifikatorn ∀ eller existenskvantifikatorn ∃ blir svårtolkade och intetsägande när de står för sig själva[2] måste vi hitta ett bra sätt att representera deras egentliga omfång (eng. scope). I och med att ∀-uttryck alltid följs av implikation och ∃-uttryck av konjunktion, kan vi abstrahera det determinativa pronomet “alla” till lambdauttrycket λP[λQ[∀x[P(x) -> Q(x)]]] och “en” till λP[λQ[∃x[P(x)∧Q(x)]]].