Konceptet Markov-modeller har dykt upp lite då och då under MLT-programmets gång och Jurafsky & Martin ägnar ett helt tilläggskapitel åt det i senaste utkastet av Speech and Language Processing (3:e upplagan 2020) på webben. Dolda Markov-modeller (eng. Hidden Markov Models, HMM) beskrivs där som en probablistisk sekvensmodell som för en given sekvens av en språklig enhet (bokstäver, morfem, ord, meningar, etc) beräknar en sannolikhetsdistribution över motsvarande etikettsekvens (t.ex. POS-taggar för varje ord i en inputmening).

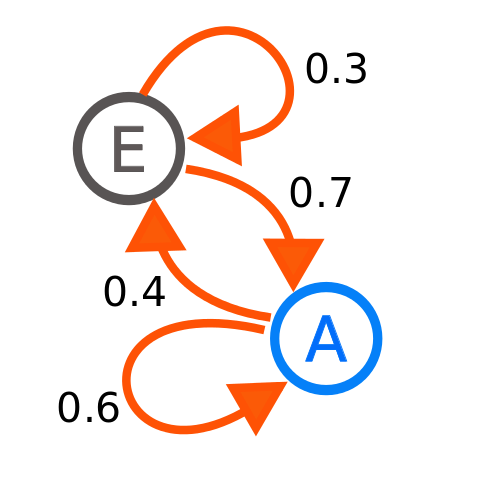
HHM beskrivs i samma kapitel som en förstärkt (eng. augmented) Markov-kedja. Den senare är en slags ändlig automat som utmärker sig genom just sannolikhetsvärderna som ges varje båge från en nod till en annan. För att beräkna nästa tillstånd i kedjan gör man Markov-antagandet att nästa tillståndsnod i sekvensen enbart är beroende av det nuvarande tillståndet (inget av de tidigare). Jurafsky & Martin beskriver det som att förutspå morgondagens väder på basis av hur det ser ut idag, och helt bortse från hur det var igår eller i förra veckan. I ett språkmodelleringssammanhang skulle det innebära att nästa ord i meningen enbart beror på det senast genererade ordet.

Joxemai4, CC BY-SA 3.0, via Wikimedia Commons

Skillnaden mellan en Markov-kedja och en dold Markov-modell (HHM) är att Markov-kedjorna enbart modellerar sannolikheten för oberserverbara händelser (som ord i en mening), men inte för dolda händelser (etiketter) som deras POS-taggar och dylikt. HHM:er kan dock göra bådadera. De följer dels antagandet om att varje tillstånd $ t_{i} $ är beroende av föregående tillstånd $ t_{i-1} $ (precis som Markov-kedjor), men också att den utdataobservation $ o_{i} $ som görs enbart är beroende av tillståndet $ t_{i} $ som genererade det (inte av andra observationer eller tillstånd).

Ett svar i den här StackExchange-tråden förklarar på ett bra sätt hur man kan applicera HHM på ett problem som taligenkänning. Med en Markov-kedja kan man skapa en språkmodell utifrån textdata som beräknar sannolikheten för varje ord i vokabuläret givet det nuvarande ordet (tillståndet). Men eftersom ord kan uttalas olika beroende på person och sammanhang går det inte att applicera den här modellen på tal rakt av. Den missar kanske att det alternativa uttalet /ɕɛks/ är detsamma som /kɛks/ och därför också referar till det (numera dolda) ordtillståndet “kex”:

“So you could get lots of people to read aloud the text that you used for your original training, you could get a distribution for the pronunciations for each word, and then combine your original model with the pronunciation model and you have a Hidden Markov Model (an HMM).” (ibid).

Sannolikheterna för de olika uttalen (observationerna) av ett givet ord (det dolda tillståndet) kallas emissionssannolikheterna, medan sannolikheterna för alla ord givet ett visst ord (alla möjliga tillstånd givet det nuvarande tillståndet) kallas transitionssannolikheter.

Fun fact: Markov-kedjor och -modeller har fått sitt namn efter den ryske matematikern Andrej Markov. Han testade sin hypotes om Markov-antagandet genom att räkna vokal- och konsonantpar i den ryska versromanen Eugen Onegin och undersöka i vilken omfattning man kunde förutspå en vokal givet en konsontant och vice versa (läs mer om det här).