Läser idag pappret “Attention is all you need” av Vaswani et al. (2017) som introducerar djupinlärningsarkitekturen Transformer. Transformer lyfts fram som ett konkurenskraftigt alternativ till återkopplande neurala nätverk (RNN), vars sekventiella natur beskrivs som ett problem för parallelliseringen av träningsexempel.

Jag var inte på det helt klara med vad det här innebär, men enligt den här Stackoverflow-tråden verkar det ha med träningshastigheten att göra. Eftersom RNN behandlar indatasträngen ord för ord och varje tidssteg är beroende av föregående tidssteg blir träningen långsam. Transformer-nätverk betraktar istället indatasekvensen som helhet och beräkningen för varje tidssteg sker oberoende av de andra.

En annan fördel som lyfts fram med Transformer gentemot RNN är hanteringen av långa dependenser, t.ex. Frankrike och franska i sekvensen “Jag växte upp i Frankrike, men nu för tiden bor jag i Boston. Jag talar flytande franska”). LSTM är en typ av RNN som utvecklades för att förbättra minneshanteringen och enbart låta relevant information flöda genom det återkopplande nätverket med hjälp av s.k. gates. Uppmärksamhets-mekanismer används ofta för att ytterligare förbättra dependenshanteringen. Trots det återstår problemet med RNN och LSTM att återkopplingen till tidigare tidssteg leder till viss informationsförlust (Jurafsky & Martin 3:e utkastet: kap 9: s. 18) och att träningen inte kan parallelliseras.

Transformer-modellen har löst det problemet genom att göra sig av med RNN-nätverkens återkoppling och istället använda en kodare-avkodare-arkitektur med flera framåtriktade nätverk samt något som kallas self-attention. Jag väljer att kalla det “självuppmärksamhet” på svenska. Jurafsky & Martin (3:e utkastet: kap 9: s. 19) beskriver självuppmärksamhet som något som “[…] allows a network to directly extract and use information from arbitrarily large contexts without the need to pass it through intermediate recurrent connections as in RNNs”. Men mer om det om en stund.

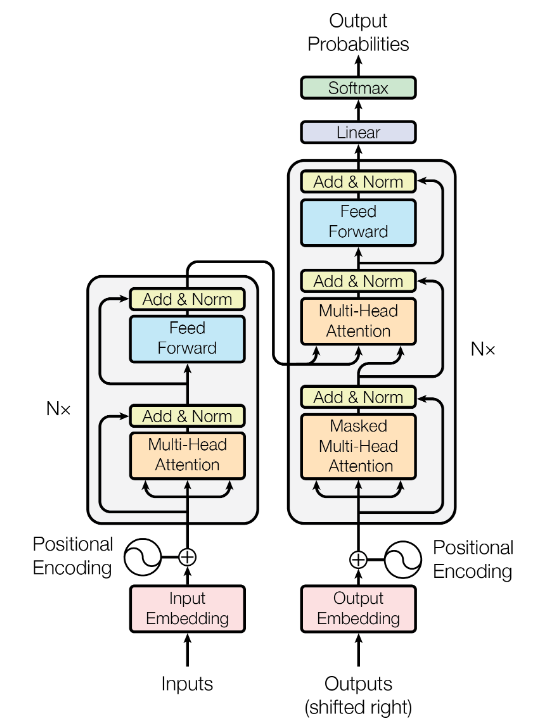
Modellarkitekturen så som den presenteras av Vaswani et al. (2017).

Bilden ovan visar Transformer-modellens arkitektur såsom den presenteras i originalpappret, med en kodare och en avkodare-del. Såväl kodaren som avkodaren består av sex identiska kodare respektive avkodare staplade på varandra (\(N = 6\)). Jurafsky & Martin använder dock inte termen “kodare” eller “avkodare” utan kallar dem block eller Transformer-block.

Varje block består av två lager: 1) ett månghövdat självuppmärksamhetslager (eng. multi-head self attention layer) och 2) ett enkelt framåtriktat lager. Dessutom tillkommer något som kallas “residual connections” eller “skip connections” vilket är ett nytt begrepp för mig men som i kort verkar gå ut på att möjliggöra för felgradienten att flöda fritt genom nätverket utan att passera en icke-linjär aktiveringsfunktion (se den här Stackoverflow-tråden för mer info). Varje lager följs även av ett normaliseringslager.

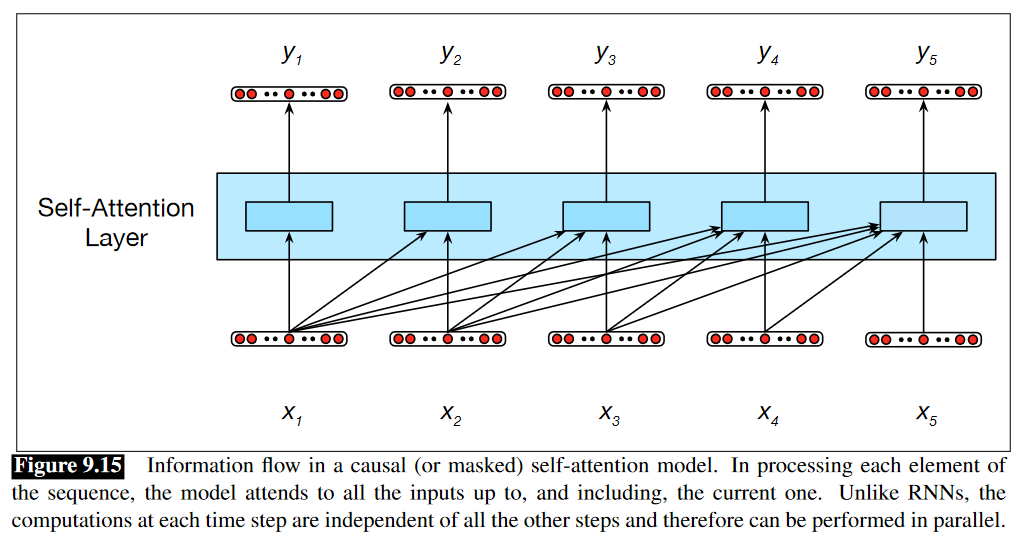
Illustration över självuppmärksamhet i Jurafsky & Martin (3:e utkastet: kap 9: s. 19).

Självuppmärksamheten går ut på att jämföra ett element $ x $ i indatasekvensen mot de föregående elementen i samma sekvens för att beräkna hur relevanta de övriga delarna är för den nuvarande kontexten (Jurafsky & Martin 3:e utkastet: kap 9: s. 19). Vaswani et al. (2017) beskriver det som att mappa en frågevektor (query, $ Q $) mot en nyckelvektor (key, $ K$) och en värdevektor (value, $ V $).

Dessa jämförelsevärden - som beräknas genom att ta den inre produkten av elementen $ x_{i} \cdot x_{j} $ - tas sedan i beaktning för att generera ett utdata $ y $. Ju högre inre produkt, desto högre likhet mellan vektorerna. Men Jurafsky & Martin poängterar att det krävs något mer för att tillföra någon form av inlärning, nämligen viktmatriser. Därför introducerar Vaswani et al. (2017) tre ytterligare parametrar till uppmärksamhetsfunktionen: en frågeviktmatris $ W^{Q} $, en nyckelviktmatris $ W^{K} $ och en värdeviktmatris $ W^{V} $. Med en frågematris $ Q = W^{Q}X $, en nyckelmatris $ K = W^{K}X $ och en värdematris $ V = W^{V}X $ ser den slutgiltiga funktionen ut så här:

\[Självuppmärksamhet(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V\]

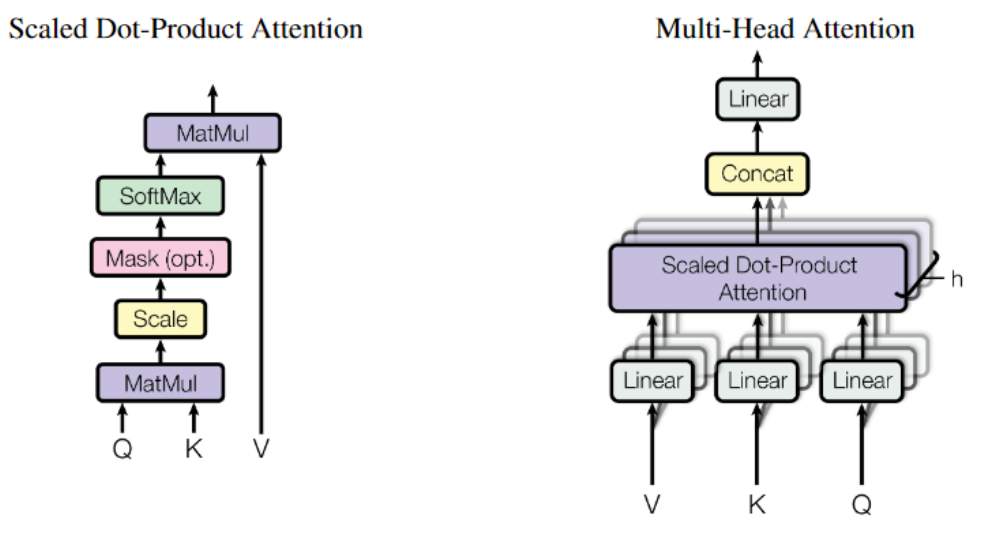
Illustration över självuppmärksamhet och månghövdad självuppmärksamhet från Vaswani et al. (2017).

Hur hänger då självuppmärksamhet och månghövdad självuppmärksamhet ihop? Jo, “huvudena” i det månghövdade självuppmärksamhetslagrena i Transformer-arkitekturen är i själva verket en samling parallella självuppmärksamhetslager som tillsammans fångar upp olika aspekter av indatasekvensen. Detta genom att varje självuppmärksamhetslager får en egen uppsättning Q-, K- och V-matriser som initieras slumpmässigt. Utdatat från varje självuppmärksamhetshuvud konkateneras sedan och reduceras till samma dimensionsstorlek som indatat.

Det är den här delen av arkitekturen som tillåter modellen att på olika sätt få bättre tillgång till övriga positioner i indatasekvensen under kodning och avkodning. Eftersom Transformer saknar RNN:ens sekventiella natur använder Vaswani et al. även positionsinbäddningar (eng. positional embeddings) som håller koll på indataelementens relativa och absoluta position i strängen.

Rekommenderad läsning

• Alammer, Jay. The Illustrated Transformer.
• Harvard NLP. The Annotated Transformer.
• Jurafsky & Martin. Deep Learning Architectures for Sequence Processing.
• Vaswani et al. Attention is all you need.